【図解】インデックスとは？高速探索を可能にする仕組み【DB】

2024年3月24日2024年4月10日

インデックスの概要

インデックスはクエリの実行に必要な時間を大幅に短縮するための仕組みの一つです。

インデックスが適切に設定されたテーブルであれば、数億レコードあるテーブルだとしても必要なデータだけを一瞬で取得することも可能にします。

インデックスはテーブル作成時に設定することもできますが、すでにレコードが格納されているテーブルにも設定可能です。そのため現在レコード数が多くてデータ取得に時間がかかり困っている方はインデックスの導入を検討すると良いでしょう。

この後、インデックスの本質を理解していただくために少しだけ深い話をします。本質を理解することによって、どのようにインデックスを張るべきなのかとインデックスを張ることのデメリットを深く理解できるからです。

大半の人はインデックスの本質を理解していない

インデックスは名前の通り本の索引によく例えられます。念のため解説しておくと、本の索引とは以下のようにキーワードとそれが載っているページをリスト形式で載せているものです。

• メダカ・・・29ページ
• メモリ・・・50, 74ページ
• モズク・・・1, 22, 33, 44, 55, 66ページ

データベースにおけるインデックスの説明に本の索引が用いられた場合の説明は以下のようなものです。

「目的のキーワードが載っているページを読みたいとき、索引が無ければ1ページ目から順番に読んで探さないといけません。しかし索引があればキーワードに該当するページを一発で知ることが出来ます。データベースでインデックスを利用すると、このように索引からすぐに特定のレコードを見つけることが出来るのです。」

確かにこの説明を聞くと一瞬なるほどと思います。でもなにかおかしくないですか？

だってそのキーワードが索引内のどこに存在するのかはちゃんと探さないと知ることが出来ないからです。

本の場合であれば1ページ1ページ丸々読む必要が消え、索引内だけを探せば済むので確認量を大きく減らせます。しかしテーブルの場合、キーワードとそのキーワードを含むレコードの組み合わせを持った索引を作ったとして、索引の中で特定のキーワードを探すことと、索引を使わずにレコードを探索することの何が違うのでしょうか？違いがありません。

だとしたらインデックスとは何なのか。

それは「索引 + 索引内の探し出したいキーワードにたどり着くためのアルゴリズムおよびデータ構造」です。

インデックスの本質を知る上で重要なのはこの後半の部分になります。

インデックスを「張る」と日本では言うことが多いため、テーブルに対してカラムを追加しちょっとしたデータを格納するようなイメージを持ってしまうかもしれません。しかし実態は全く異なります。インデックスを張るということの本当の意味は「索引内のキーワードを超効率的に見つけられるデータ構造のオブジェクトを作る」ことを指すのです。

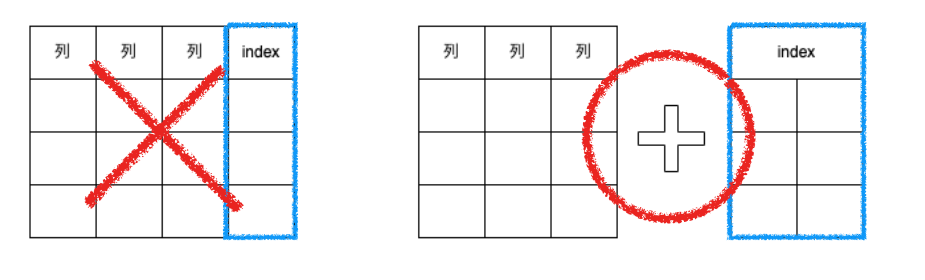
インデックスはテーブルに何かをちょい足しするようなものではないことを理解しておきましょう。ちなみに「張る」という表現をするのは日本だけで、英語では"create an index"や"add an index"と呼びます。

ではインデックスとはどのようなデータ構造を持つのでしょうか？たくさんの種類があるのですが、この記事では代表的な二つを紹介します。

代表的なインデックスのデータ構造

データベースのインデックスに用いられる代表的なデータ構造を紹介します。紹介するのは以下の2つです。

• B+Treeインデックス
• ハッシュインデックス

他のデータ構造についてもこの2つのデータ構造がもとになっているものが大半なので、まずはこの二つを理解しましょう。

B+Treeインデックス

超有名なデータベースであるOracle DB、MySQL、PostgreSQLで採用されているデータ構造です。

仕組みは二分探索の応用です。二分探索とは、探したいものがあるときに候補の数が半分になるように探索を繰り返す手法になります。例えば1~100の数値の中から23を見つけたいときには、まず1と100の間である50よりも大きいか小さいかで判断し、小さいことが分かったら今度は1と50の中間である25よりも大きいか小さいかで判断する、同じ流れで目的の23のみに絞られるまで繰り返す、といった流れです。

もし単純に先頭から探すという手法を取った場合、1を探すのであれば一瞬で終わりますが100を探すときに時間がかかってしまいます。しかし二分探索の場合はどんな数字が来た時にもある程度少ない探索数で見つけたい数字を見つけることが出来ます。

それでは本題のB+treeの構造について説明します。二分探索との違いは大きいか小さいかのような二択だけではなくそれ以上の択を設定できるポイントにあります。以下にB+Treeの構造を簡単な図で表します。

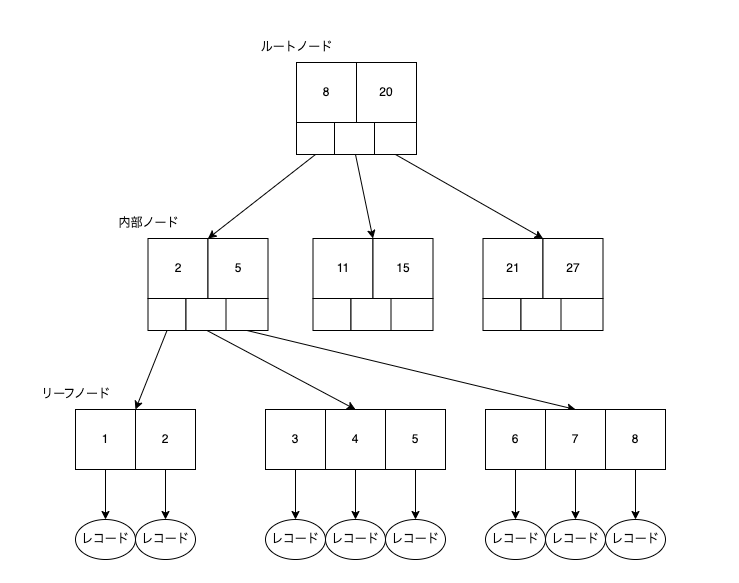
B+Treeを構成する要素は以下の3つです。

• ルートノード：一番上部のノード。最初に探索対象になる。
• 内部ノード：ノードとノードを紐づけるノード。ルートノードでの分岐をさらに詳細化するために存在。ルートノードとリーフノードは1層のみだが、内部ノードはデータ量によっては複数層になることもある。
• リーフノード：レコードに直接紐づいているノード

各ノードはキーというものを持っています。上の図で言うと各ノード内に記載されている数字がキーに該当します。ルートノードと内部ノードが持つキーは次にどのノードに行くべきかを表しており、リーフノードが持つキーは直接レコードの位置と紐づいています。

見つけるまでの流れは以下です。

1. ルートノード内のキーを左から確認し、探索対象の値以上のキーが見つける
2. 大きいキーが見つかったらキーの左下の箱から出ている矢印に従い子ノードに移動する。もし見つからなければ一番右側の箱から出ている矢印に従う
3. 2を繰り返してリーフノードに辿り着く

前提

リーフノードの並びおよびリーフノード内のキーの並びは何かしらの基準でソートされています。保存対象が数値ではなく文字列だとしてもA→Zのように何かしらの基準をもってソートされます。だからこそ二分探索の時と同じようにB+Tree構造で高速な検索ができるのです。

しかし常にソートされた状態を維持するためにレコードの挿入や更新時にノードの分割や並びに気を付けたキーの挿入などの処理が必要です。B+Treeはこういったレコード操作にも効率よく対応できるようなロジックにはなっていますが、少なからず処理の負荷はあります。

インデックスの張りすぎはレコード操作時に悪影響を与えてしまうので、追加する必要があるのかはよく吟味しましょう。

※ インデックスの張り方については別の記事にて説明予定です。

ハッシュインデックス

ハッシュインデックスはNoSQLデータベースや主キーに設定されるインデックスに利用されることが多いインデックスです。

範囲検索（~以上や~未満など）は不可なので利用できる場所は限られるのですが、等価検索（where id=5のようにイコールを用いた検索）ではB+Treeよりも高速なので、範囲検索が行われにくい主キーのようなカラムに設定すると強いインデックスです。

仕組みはとても単純です。ハッシュテーブルというものを利用します。ハッシュテーブルにおける重要な要素は以下の2つです。

• ハッシュ値：ハッシュテーブル内の位置を指す
• ハッシュ関数：レコード内の特定のカラムの情報をハッシュ値に変換する関数

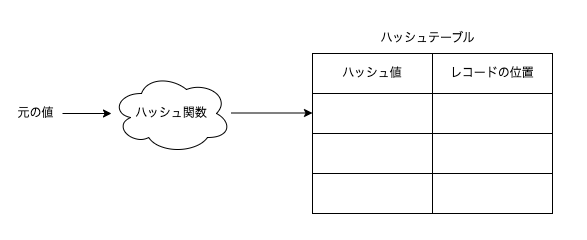
ハッシュテーブルはインデックス作成時に作成されるもので、ハッシュ値はハッシュテーブル内の位置を指しています。レコードが追加・更新された際にはインデックスに設定されたカラムの値がハッシュ関数によりハッシュ値に変換され、レコードの位置とセットでハッシュテーブルに格納されます。

検索時には検索に利用された値をハッシュ関数でハッシュ値に変換したら、その値からすぐに対象のレコードの位置を特定可能です。

ただしハッシュ値は規則的に並んでいるわけではないためピンポイントで見つけることしかできず、～以上のような範囲検索は不可になります。

まとめ

この記事で最も重要なポイントは、インデックスとは「索引 + 索引内の探し出したいキーワードにたどり着くためのアルゴリズムおよびデータ構造」のことを指すという点です。ぜひこのポイントだけでも覚えておいてください。

インデックスにより高速探索を可能にする仕組みと設定し過ぎが良くない理由を理解できていると思いますので、今後DB設計の際に役立つと思います。

別の記事にてどのようにインデックスを設定すべきなのかも解説する予定なので、お楽しみに。

参考記事

• 第7回　性能改善の鍵、インデックスの特性を知る～B-treeとハッシュ　（1）B-tree | gihyo.jp
• DBのインデックスを理解しよう

おすすめ書籍

DBのスペシャリストになりたい人向けのバイブル。